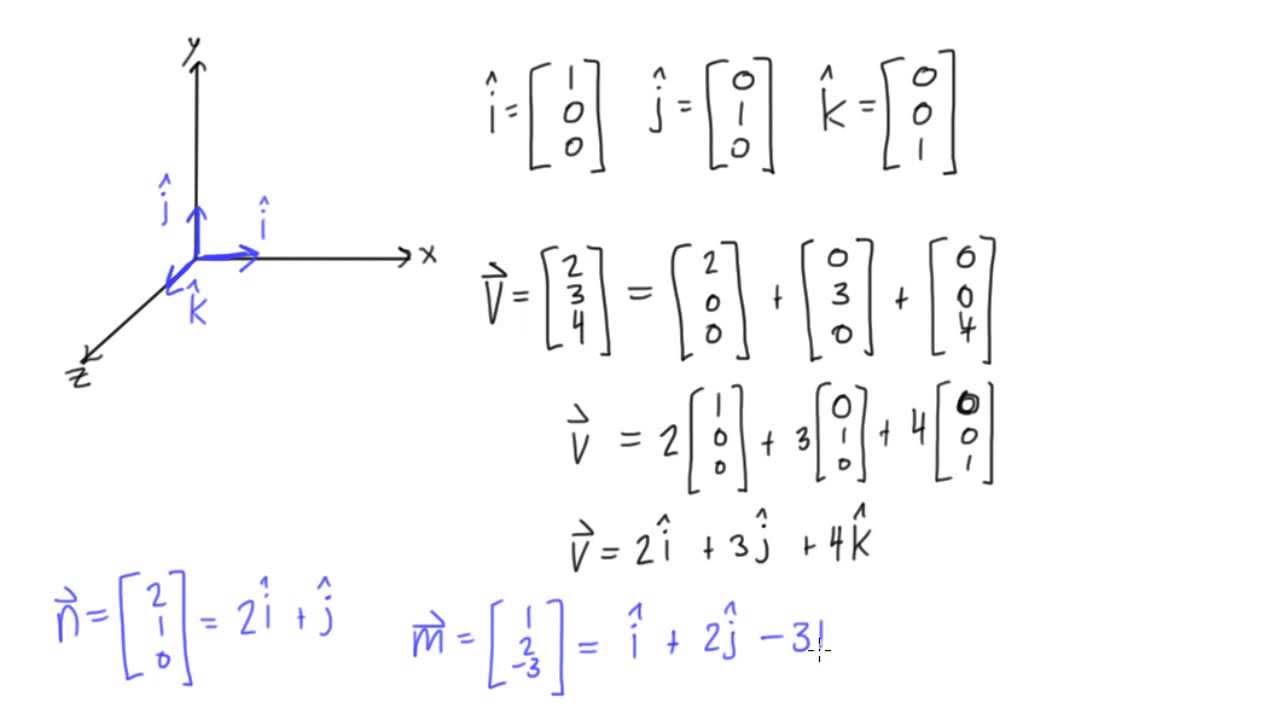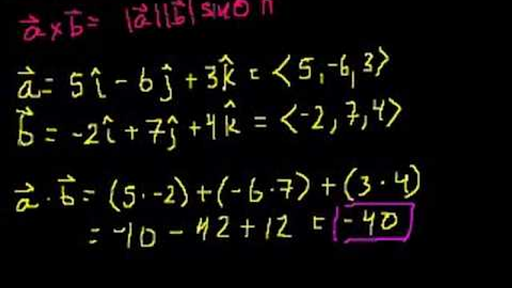I J K Vector Notation

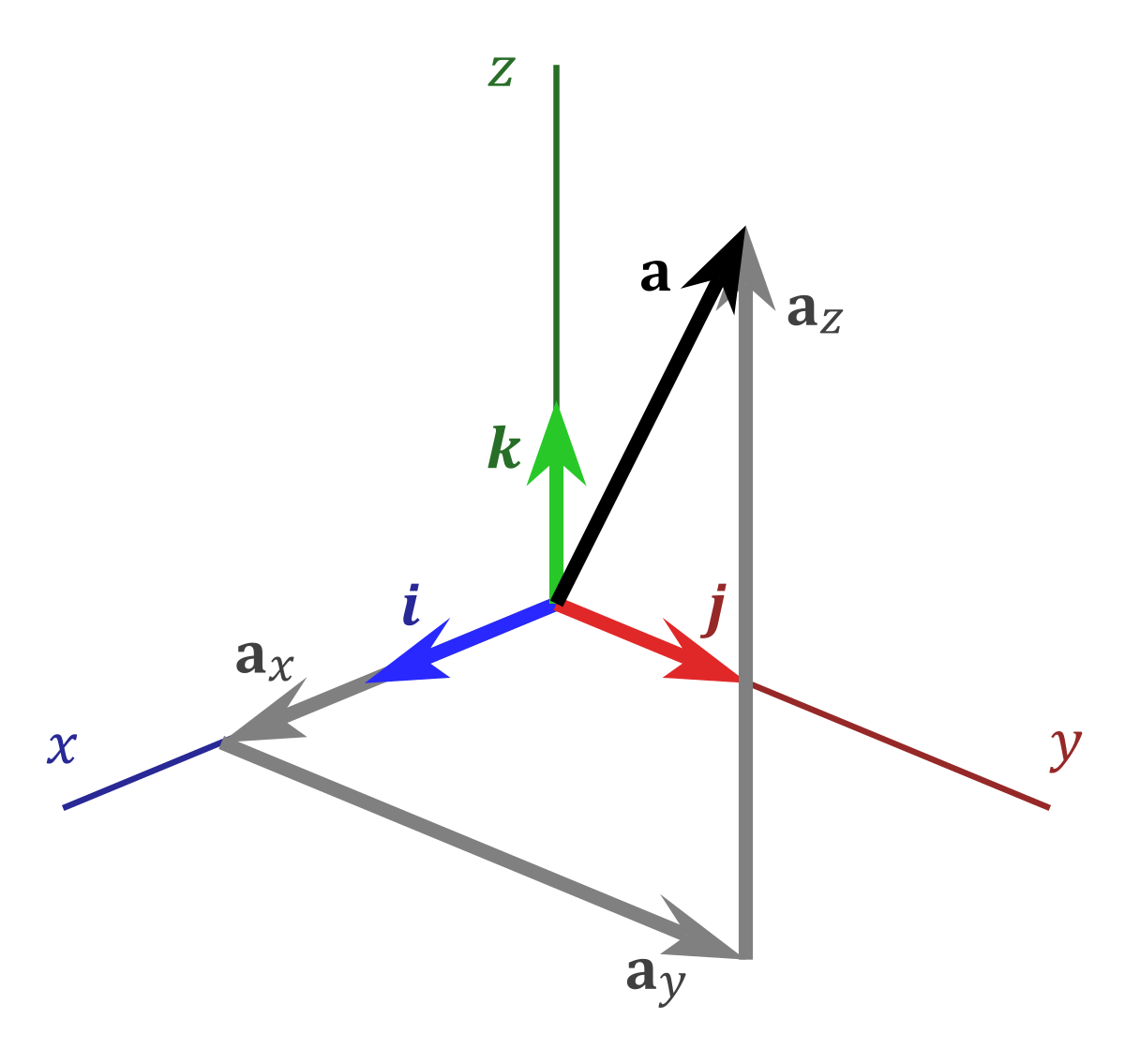
I j and k are just the unit vectors of the x y and z directions.

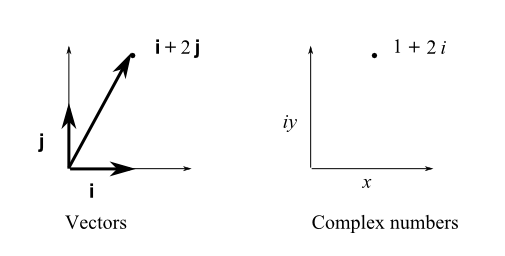
I j k vector notation. The symbols i j and k are typically used to denote unit vectors in cartesian x y z coordinate systems. 2i 11 j the position vector of ship a is. Vectors have magnitude and direction. Applying this corollary to the unit vectors means that the dot product of any unit vector with itself is one.

Vector notation is a commonly used mathematical notation for working with mathematical vectors which may be geometric vectors or members of vector spaces. Vector a starts at point 1 2 3 and goes to point 4 5 6. Unit vector i is taken parallel to the x axis j parallel to the y axis and k parallel to the z axis. And that is the same thing but in the y direction.

And i m going to define another vector and that one is called j. I 11 j km a b i 11 j 2i 11 j 3i. Image transcriptionclose 3 using the i j k vector notation what is the vector created by adding together two vectors a and b. Ijk notation is a way of writing the vector in terms of its components.

What is ijk notation. I i j j k k 1 1 cos 0 1. A a aa cos 0 a2. And that is probably how you saw them written last year.

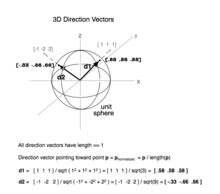
There are three symbols used in this way because many problems are best expressed in a three dimensional vector space. For representing a vector the common typographic convention is lower case upright boldface type as in and. The international organization for standardization iso recommends either bold italic serif as in v or a or non bold italic. In addition since a vector has no projection perpendicular to itself the dot product of any unit vector with any other is zero.

But if you see i and not in the imaginary number sense you should realize that that s the unit vector. So it will have the position vector. In engineering notation you re essentially just breaking down the vector into its x y and z components. When a unit vector in space is expressed in cartesian notation as a linear combination of i j k its three scalar components can be referred to as direction cosines.

The position vector of a relative to b the position vector of ship a the position vector of ship b the position vector of ship b will be the same as it does not change velocity. So let s say vector a is 5i i is just the unit vector in the x direction minus 6j plus 3k. The value of each component is equal to the cosine of the angle formed by the unit vector with the respective basis vector. There s some other notations.