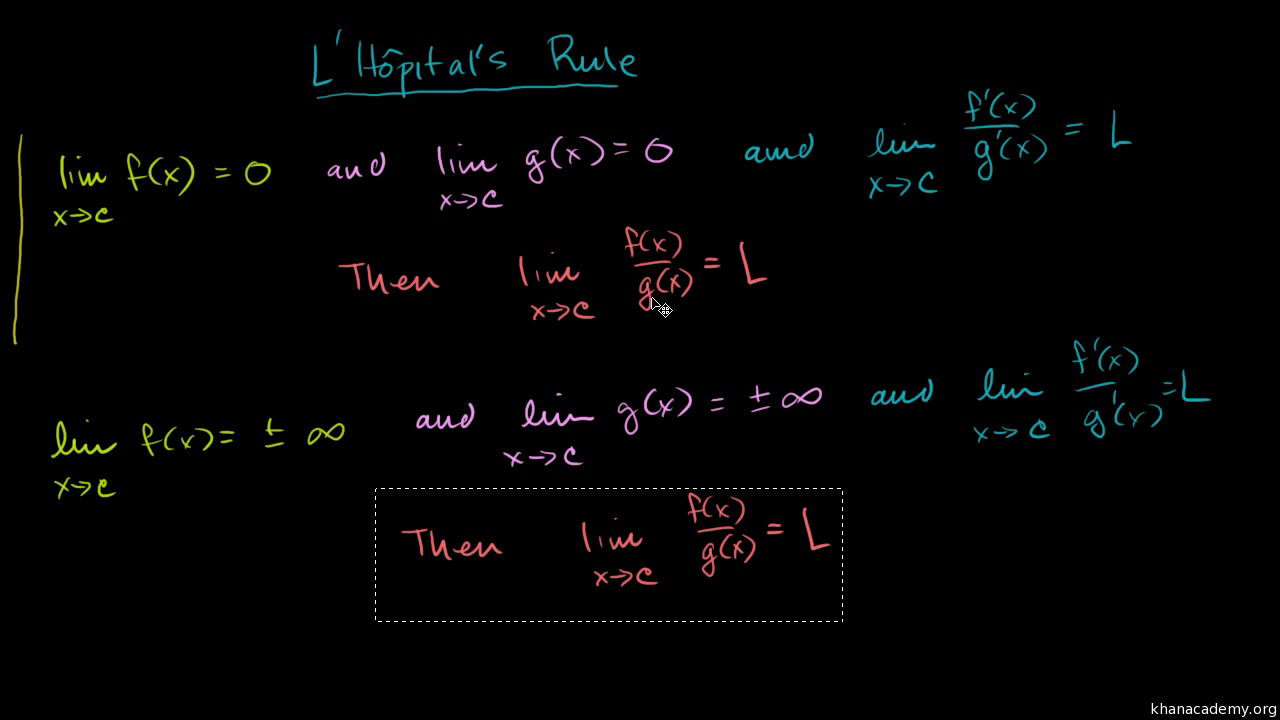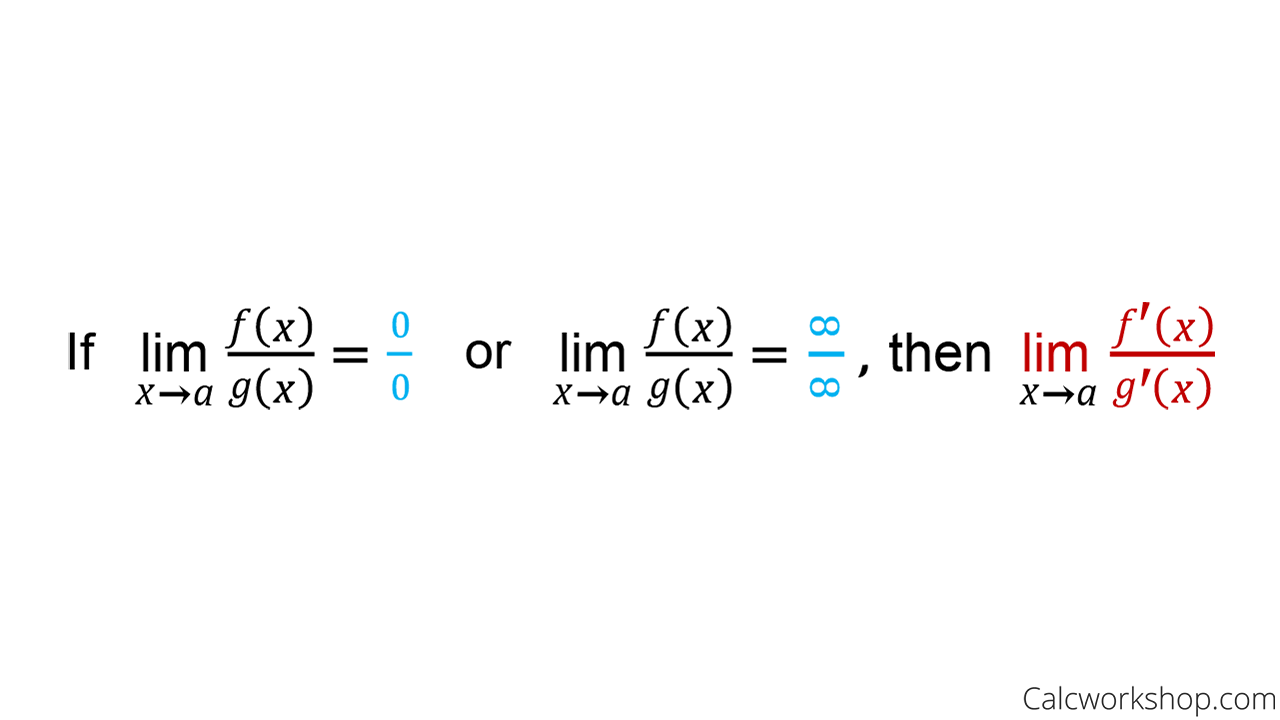L Hopital S Rule Calculus

L hôpital is pronounced lopital who was a french mathematician from the 1600s.

L hopital s rule calculus. L hôpital s rule helps us find many limits where direct substitution ends with the indeterminate forms 0 0 or. L hospital s rule also spelled l hôpital s is a way to find limits using derivatives when you have indeterminate limits e g. Then we need to apply l hôpital s rule. Lim xsinx x2 4x2 x 2pi x 2pi 1a.

The rule is named after the 17th century french mathematician guillaume de l hôpital. L hôpital s rule for displaystyle frac infty infty suppose lim f x and lim g x are both infinite. If we try to evaluate the limit directly it results in indeterminate form. Lim xsinx x2 4x2 x 2pi x 2pi use l hopital s rule to find the limit.

It says that the limit when we divide one function by another is the same after we take the derivative of each function with some special conditions shown later. Lim x 0 d d x 1 cos x d d x x 2 lim x to0 left frac frac d dx left 1 cos left x right right frac d dx left x 2 right right x 0lim. Although the rule is often attributed to l hôpital the theorem was first introduced to him in 1694. It is important to realize that we are not calculating the derivative of the quotient fg fg.

Note that l hôpital s rule states we can calculate the limit of a quotient fgfgby considering the limit of the quotient of the derivatives f g f g. The more modern spelling is l hôpital. Before proceeding with examples let me address the spelling of l hospital. If you re seeing this message it means we re having trouble loading external resources on our website.

So l hospital s rule tells us that if we have an indeterminate form 0 0 or all we need to do is differentiate the numerator and differentiate the denominator and then take the limit. If the numerator and the denominator both tend to infty or infty l hôpital s rule still applies. Use l hopital s rule to find the limit. In mathematics more specifically calculus l hôpital s rule or l hospital s rule french.

Calculus q a library 1a. Review how and when it s applied. L hôpital s rule can help us calculate a limit that may otherwise be hard or impossible. L hospital s rule doesn t work in all cases.

In those cases the usual ways of finding limits just don t work. Application or repeated application of the rule often converts an indeterminate form to an expression that can be easily evaluated by substitution.